🃏 Permutation Test for Two Proportions
Test Proportions
Introduction
We saw from the diagram created by Allen Downey that there is only one test! We will now use this philosophy to develop a technique that allows us to mechanize several Statistical Models in that way, with nearly identical code.
We will use two packages in R, mosaic and the relatively new infer
package, to develop our intuition for what are called permutation
based statistical tests.
Testing for Two or More Proportions
Let us try a dataset with Qualitative / Categorical data. This is the
General Social Survey GSS dataset, and we have people with different
levels of Education stating their opinion on the Death Penalty. We
want to know if these two Categorical variables have a correlation, i.e.
can the opinions in favour of the Death Penalty be explained by the
Education level?
Since data is Categorical ( both variables ), we need to take counts
in a table, and then implement a chi-square test. In the test, we will
permute the Education variable to see if we can see how significant
its effect size is.
##
## categorical variables:
## name class levels n missing
## 1 Region factor 7 2765 0
## 2 Gender factor 2 2765 0
## 3 Race factor 3 2765 0
## 4 Education factor 5 2760 5
## 5 Marital factor 5 2765 0
## 6 Religion factor 13 2746 19
## 7 Happy factor 3 1369 1396
## 8 Income factor 24 1875 890
## 9 PolParty factor 8 2729 36
## 10 Politics factor 7 1331 1434
## 11 Marijuana factor 2 851 1914
## 12 DeathPenalty factor 2 1308 1457
## 13 OwnGun factor 3 924 1841
## 14 GunLaw factor 2 916 1849
## 15 SpendMilitary factor 3 1324 1441
## 16 SpendEduc factor 3 1343 1422
## 17 SpendEnv factor 3 1322 1443
## 18 SpendSci factor 3 1266 1499
## 19 Pres00 factor 5 1749 1016
## 20 Postlife factor 2 1211 1554
## distribution
## 1 North Central (24.7%) ...
## 2 Female (55.6%), Male (44.4%)
## 3 White (79.1%), Black (14.8%) ...
## 4 HS (53.8%), Bachelors (16.1%) ...
## 5 Married (45.9%), Never Married (25.6%) ...
## 6 Protestant (53.2%), Catholic (24.5%) ...
## 7 Pretty happy (57.3%) ...
## 8 40000-49999 (9.1%) ...
## 9 Ind (19.3%), Not Str Dem (18.9%) ...
## 10 Moderate (39.2%), Conservative (15.8%) ...
## 11 Not legal (64%), Legal (36%)
## 12 Favor (68.7%), Oppose (31.3%)
## 13 No (65.5%), Yes (33.5%) ...
## 14 Favor (80.5%), Oppose (19.5%)
## 15 About right (46.5%) ...
## 16 Too little (73.9%) ...
## 17 Too little (60%) ...
## 18 About right (49.7%) ...
## 19 Bush (50.6%), Gore (44.7%) ...
## 20 Yes (80.5%), No (19.5%)
##
## quantitative variables:
## name class min Q1 median Q3 max mean sd n missing
## 1 ID integer 1 692 1383 2074 2765 1383 798.3311 2765 0Note how all variables are Categorical !! Education has five levels:
## Education n
## 1 Left HS 400
## 2 HS 1485
## 3 Jr Col 202
## 4 Bachelors 443
## 5 Graduate 230
## 6 <NA> 5## DeathPenalty n
## 1 Favor 899
## 2 Oppose 409
## 3 <NA> 1457Let us drop NA entries in Education and Death Penalty. And set up a table for the chi-square test.
## [1] 1307 2## # A tibble: 10 × 5
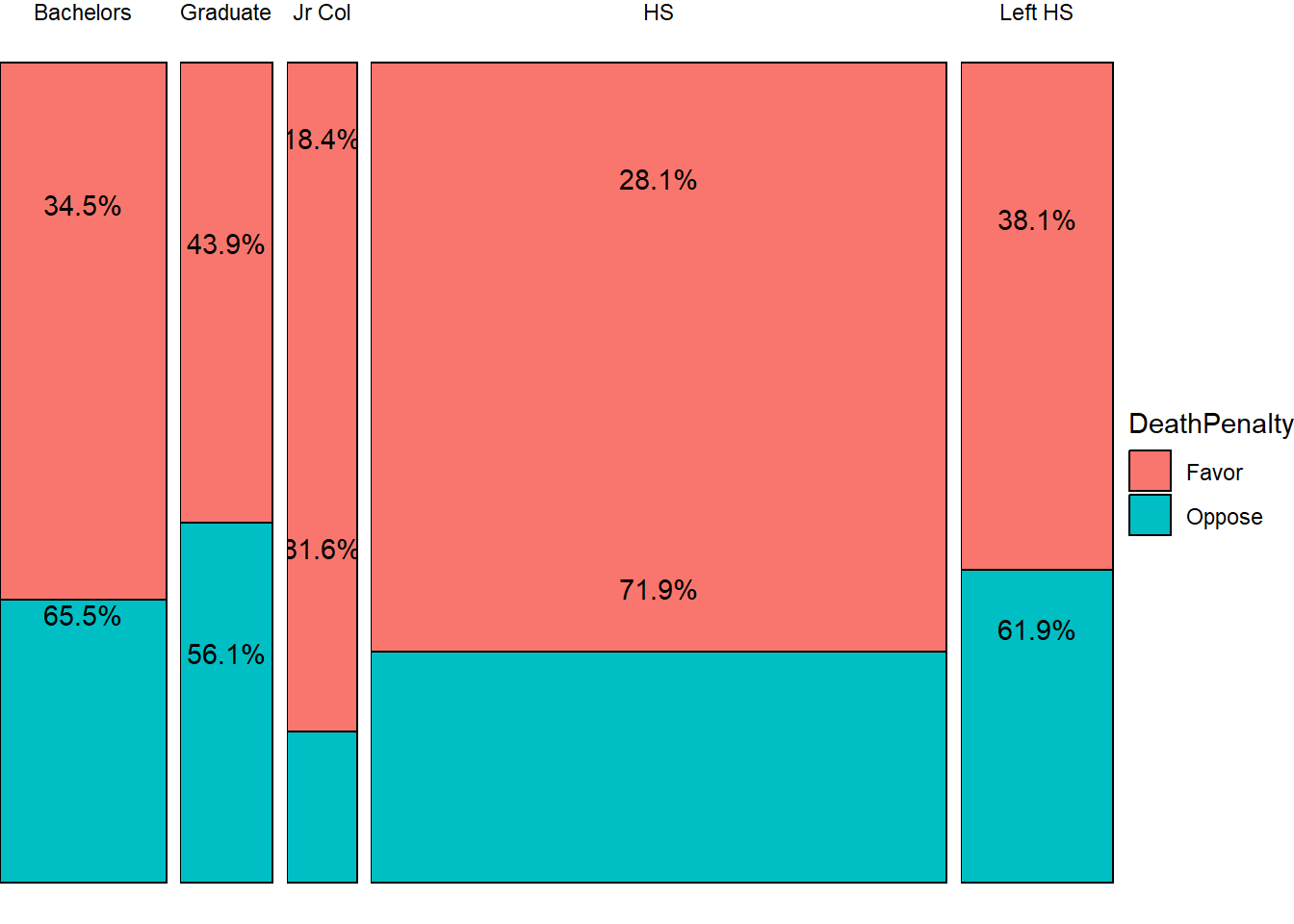
## Education DeathPenalty count edu_count edu_prop
## <fct> <fct> <int> <int> <dbl>
## 1 Bachelors Favor 135 206 0.655
## 2 Bachelors Oppose 71 206 0.345
## 3 Graduate Favor 64 114 0.561
## 4 Graduate Oppose 50 114 0.439
## 5 Jr Col Favor 71 87 0.816
## 6 Jr Col Oppose 16 87 0.184
## 7 HS Favor 511 711 0.719
## 8 HS Oppose 200 711 0.281
## 9 Left HS Favor 117 189 0.619
## 10 Left HS Oppose 72 189 0.381Table Plots
We can plot a heatmap-like mosaic chart for this table.
Using ggplot
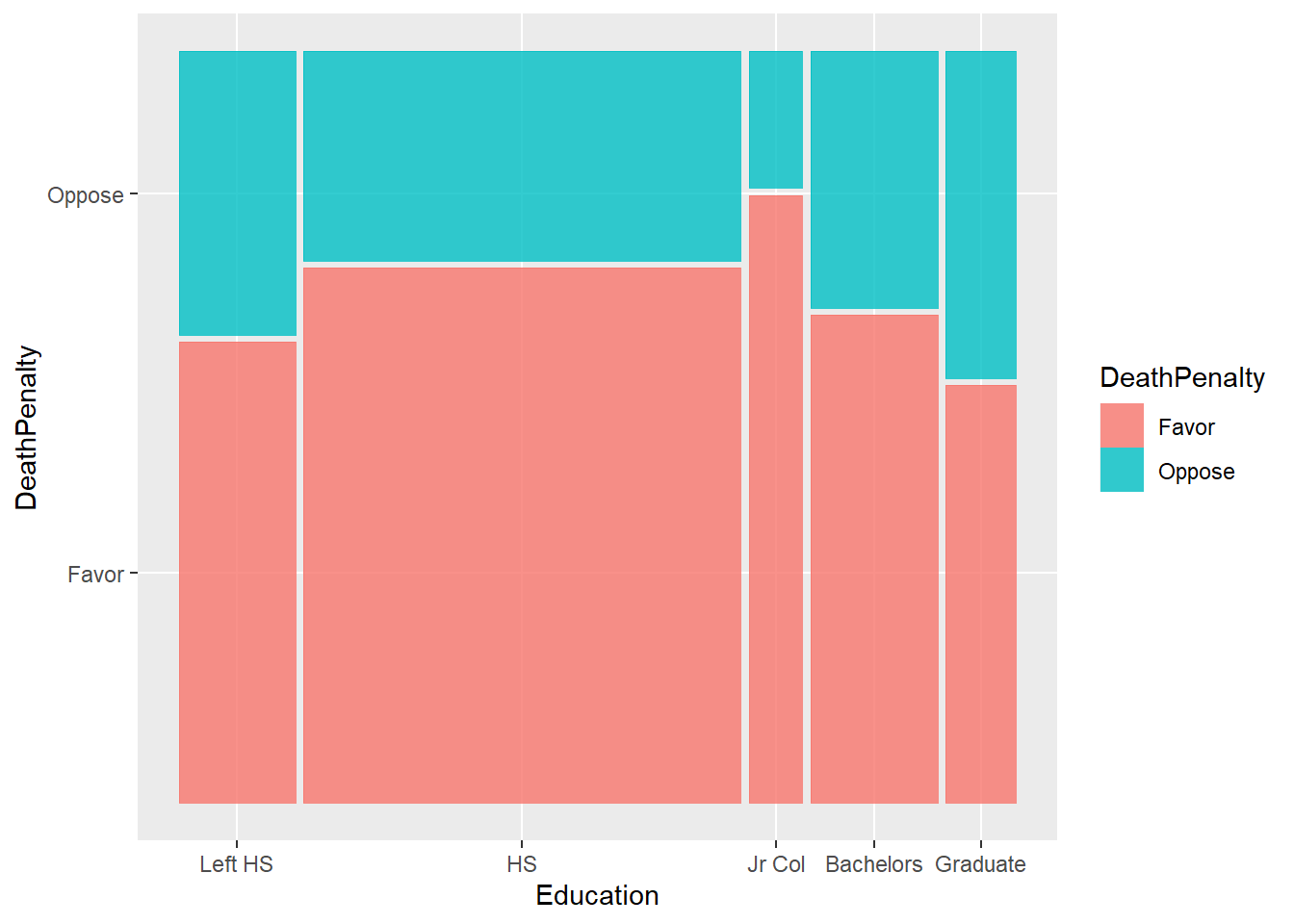
Using ggmosaic
Observed Statistic: the X^2 metric
When there are multiple proportions involved, the X^2 test is what is used.
Let us now perform the base chisq test: We need a table and then the
chisq test:
## Education
## DeathPenalty Left HS HS Jr Col Bachelors Graduate
## Favor 117 511 71 135 64
## Oppose 72 200 16 71 50## X.squared
## 23.45093##
## Pearson's Chi-squared test
##
## data: tally(DeathPenalty ~ Education, data = gss2002)
## X-squared = 23.451, df = 4, p-value = 0.0001029What would our Hypotheses be?
$$ H_0: Education Does Not affect Votes on Death Penalty\
H_a: Education affects Votes on Death Penalty
$$
We should now repeat the test with permutations on Education:
## X.squared df p.value method alternative
## X-squared...1 1.1268272 4 0.8899928 Pearson's Chi-squared test NA
## X-squared...2 6.1348278 4 0.1893030 Pearson's Chi-squared test NA
## X-squared...3 10.1774328 4 0.0375426 Pearson's Chi-squared test NA
## X-squared...4 3.9776503 4 0.4090390 Pearson's Chi-squared test NA
## X-squared...5 3.9712187 4 0.4099150 Pearson's Chi-squared test NA
## X-squared...6 0.3383714 4 0.9872044 Pearson's Chi-squared test NA
## data .row
## X-squared...1 tally(DeathPenalty ~ shuffle(Education), data = gss2002) 1
## X-squared...2 tally(DeathPenalty ~ shuffle(Education), data = gss2002) 1
## X-squared...3 tally(DeathPenalty ~ shuffle(Education), data = gss2002) 1
## X-squared...4 tally(DeathPenalty ~ shuffle(Education), data = gss2002) 1
## X-squared...5 tally(DeathPenalty ~ shuffle(Education), data = gss2002) 1
## X-squared...6 tally(DeathPenalty ~ shuffle(Education), data = gss2002) 1
## .index
## X-squared...1 1
## X-squared...2 2
## X-squared...3 3
## X-squared...4 4
## X-squared...5 5
## X-squared...6 6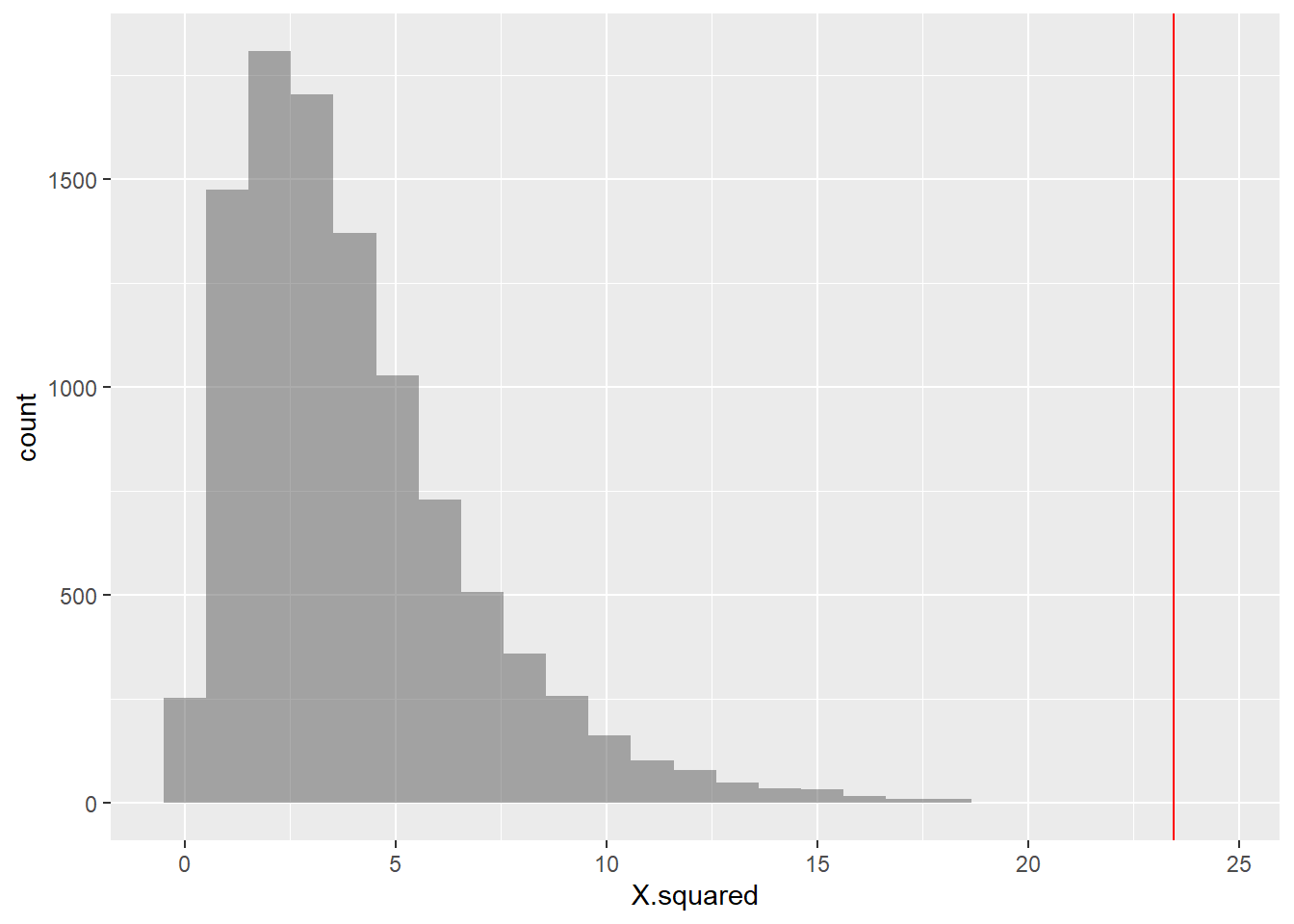
## prop_TRUE
## 0.00019998The p-value is well below our threshold of $0.05%, so we would
conclude that Education has a significant effect on DeathPenalty
opinion!