∝ Simulation Tests
What is meant by a Simulation Test

Introduction: The Lady who Drank Tea
There is a famous story about a lady who claimed that tea with milk tasted different depending on whether the milk was added to the tea or the tea added to the milk. The story is famous because of the setting in which she made this claim. She was attending a party in Cambridge, England, in the 1920s. Also in attendance were a number of university dons and their wives. The scientists in attendance scoffed at the woman and her claim. What, after all, could be the difference?
All the scientists but one, that is. Rather than simply dismiss the woman’s claim, he proposed that they decide how one should test the claim. The tenor of the conversation changed at this suggestion, and the scientists began to discuss how the claim should be tested. Within a few minutes cups of tea with milk had been prepared and presented to the woman for tasting.
At this point, you may be wondering who the innovative scientist was and what the results of the experiment were. The scientist was R. A. Fisher, who first described this situation as a pedagogical example in his 1925 book on statistical methodology1. Fisher developed statistical methods that are among the most important and widely used methods to this day, and most of his applications were biological.
Game
Let’s try an experiment. I’ll flip 10 coins. You guess which are heads and which are tails, and we’ll see how you do. Please write down a sequence of “H” or “T”. Comparing with your classmates, we will undoubtedly see that some of you did better and others worse.
What would be your impression of one of you got 9 guesses correct? Is that SKILL or is that something else? What would be your immediate reaction and next move?
Analysis
Back to the Lady who drank Tea !!
Let’s suppose we decide to test the lady with ten cups of tea. We’ll flip a coin to decide which way to prepare the cups. If we flip a head, we will pour the milk in first; if tails, we put the tea in first. Then we present the ten cups to the lady and have her state which ones she thinks were prepared each way.
It is easy to give her a score (9 out of 10, or 7 out of 10, or whatever it happens to be). It is trickier to figure out what to do with her score. Even if she is just guessing and has no idea, she could get lucky and get quite a few correct – maybe even all 10. But how likely is that?
Now let’s suppose the lady gets 9 out of 10 correct. That’s not perfect, but it is better than we would expect for someone who was just guessing. On the other hand, it is not impossible to get 9 out of 10 just by guessing.
So here is Fisher’s great idea: Let’s figure out how hard it is to get 9 out of 10 by guessing. If it’s not so hard to do, then perhaps that’s just what happened ( that she was guessing ), so we won’t be too impressed with the lady’s tea tasting ability. On the other hand, if it is really unusual to get 9 out of 10 correct by guessing, then we will have some evidence that she must be able to tell something ( and has an unusual Skill).
But how do we figure out how unusual it is to get 9 out of 10 just by guessing? Let’s just flip a bunch of coins and keep track. If the lady is just guessing, she might as well be flipping a coin.
So here’s the plan. We’ll flip 10 coins. We’ll call the heads correct guesses and the tails incorrect guesses.
## heads
## 0 1 2 3 4 5 6 7 8 9 10
## 9 106 463 1178 2024 2438 2080 1198 410 86 8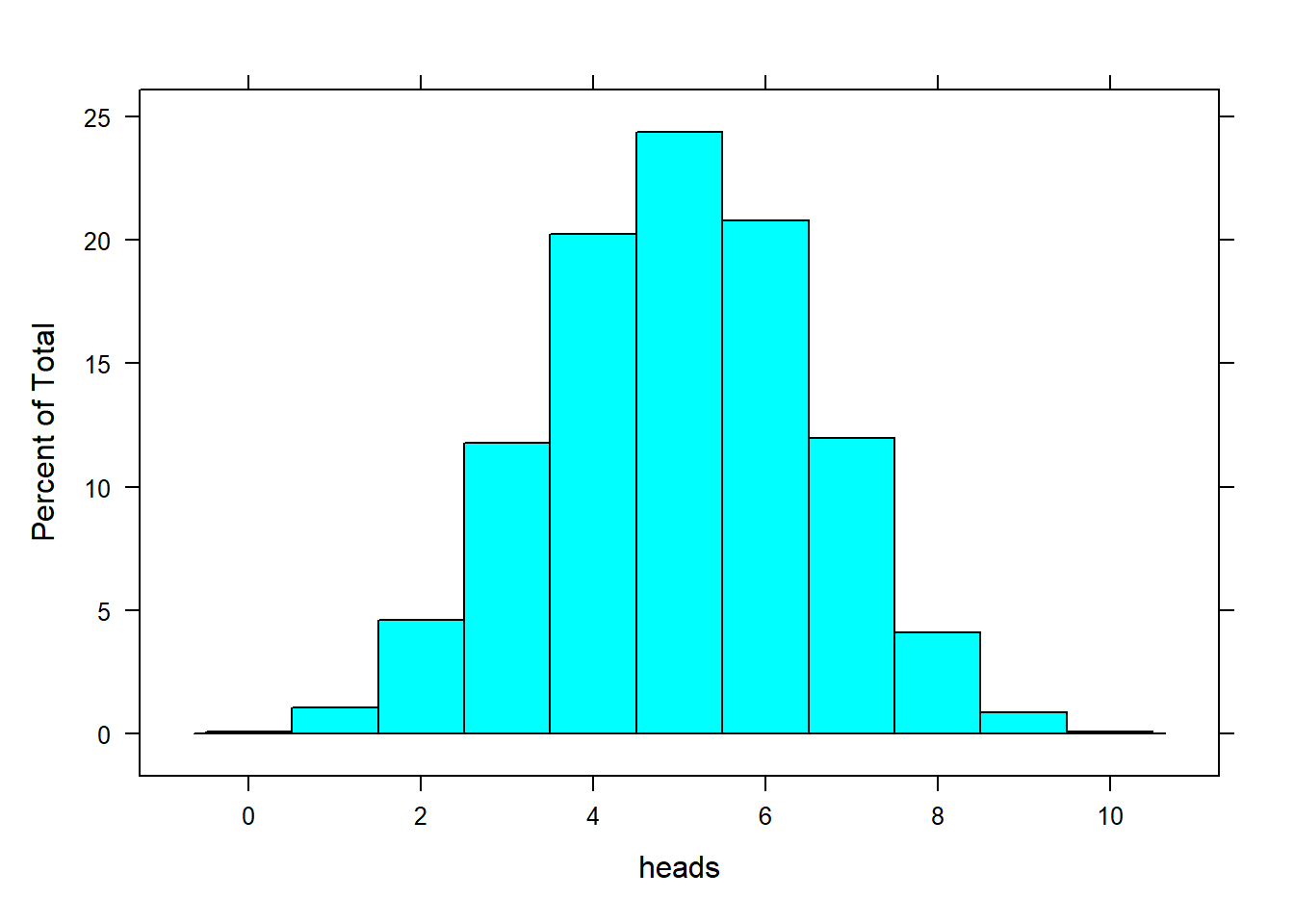
So what do we conclude? It is possible that the lady could get 9 or 10 correct just by guessing, but it is not very likely (it only happened in about 3% of our simulations). So one of two things must be true:
• The lady got unusually "lucky”, or
• The lady is not just guessing
Commentary
First we realize something is surprising, and that we have a question or doubt. This is based on something we see, or measure, a test statistic. In our story, it is the score of \(10/10\) that the Lady was able to achieve about how the Tea was made.
We then assume the Lady is guessing and somehow by chance able to guess correctly. This would be our….NULL Hypothesis. This is our (conservative) belief about the Real World.
We then randomly generate many Parallel Counterfactual Worlds, where we repeat the experiment many many times, each time calculating the test statistic, under the assumption of the NULL Hypothesis is TRUE.
We see how often our Parallel Worlds can mimic or exceed Real World measurement of the the test statistic by comparison. If this is common (i.e. probability is high) we say we cannot reject the NULL Hypothesis (and the Lady is lucky). If the occurrence is rare, as in our case, we say we have reason to reject the NULL Hypothesis and reason to believe an underlying pattern (and Lady’s ability is beyond Question !)
This is the essence of the Simulation Method in statistical modelling. Take one more look at the picture from Allen Downey’s blog2, below:

Conclusion
References
Laura Chihara, Tim Hesterberg, Mathematical Statistics with Resampling and R, Wiley, 2019.
Daniel Kaplan, Statistical Modelling, Available free on the web. https://dtkaplan.github.io/SM2-bookdown/
Russell A. Poldrack, Statistical Thinking for the 21st Century. Available free on the web. https://statsthinking21.github.io/statsthinking21-core-site/
Mine Çetinkaya-Rundel & Johanna Hardin, An Introduction to Modern Statistics, Available free on the web. https://www.openintro.org/book/ims/.
Start Teaching Stats with R, by the Mosaic Project. All about the
mosaicpackage in R. Available free on the web. https://github.com/ProjectMOSAIC/LittleBooks/raw/master/Starting/MOSAIC-StartTeaching.pdfD. Salsburg. The Lady Tasting Tea: How statistics revolutionized science in the twentieth century. W.H. Freeman, New York, 2001
R.A. Fisher. Statistical Methods for Research Workers. Oliver & Boyd, 1925↩︎
Allen Downey, There is still only one test, https://allendowney.blogspot.com/2016/06/there-is-still-only-one-test.html↩︎