🕹 A Random Walk with Hamlet
The Science of Surprise
Let us then examine the street traffic data we have gathered for any
“model-like” pattern! Is our data clean? Do we have two columns of data,
one containing 60counts of vehicles, and the other containing
inter-vehicular gap times in seconds?
We will use a tool called, ah…umm…ahem…er…WTFcsv. Let us
first quickly see what this tool offers us!
Let us import our data into the WTFcsv tool and see what patterns lurk beneath our data!
Discussion-1
- There were similar patterns in everybody’s data 😮
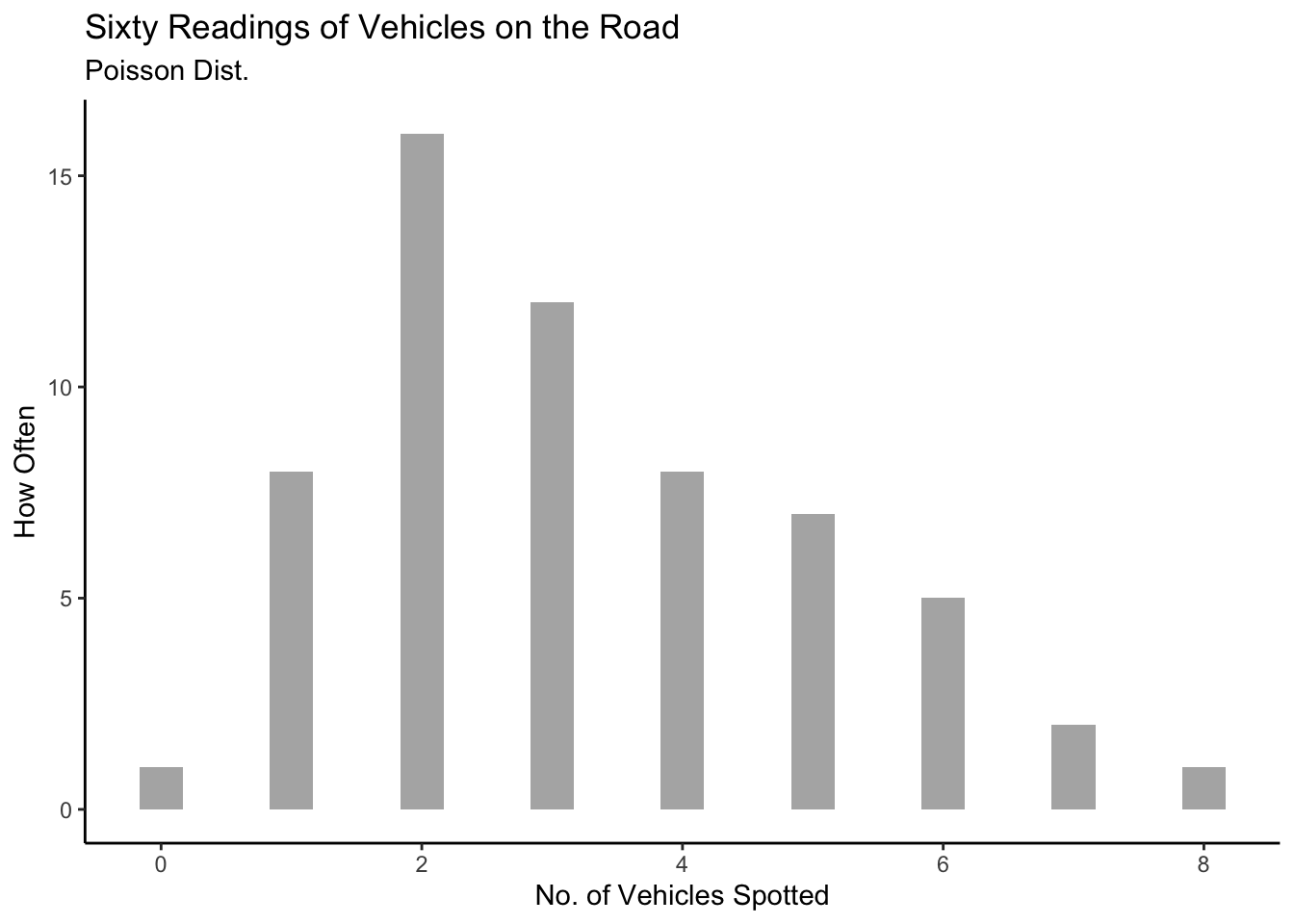
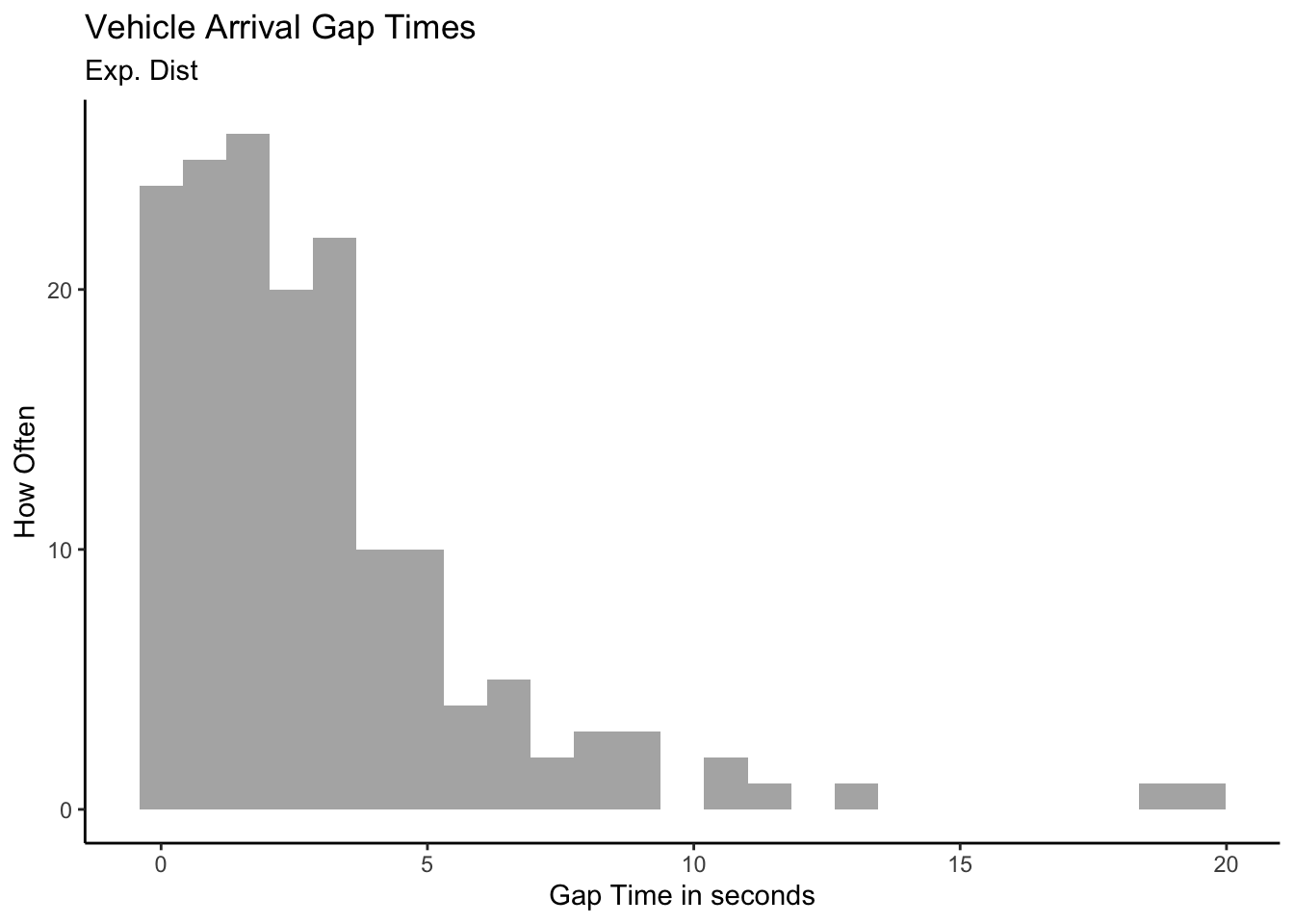
- What we saw was an example of the Poisson Arrival Process.
- This has applications in Service Design, Traffic Management, Logistics, Finding Defects in Materials, Weather Modelling, Pest Control…
From https://stats.stackexchange.com/a/297375:
(Say) Lambda(
) is the average number of cars that pass per unit of time, let’s say 60/hour ( = 60). We know, however, that the actual number will vary - some days more, some days less. The Poisson Distribution allows us to model this variability. Now, an average of 60 cars per hour equates to an average of 1 car passing by each minute. Again though, we know there’s going to be variability in the amount of time between arrivals: Sometimes more than 1 minute; other times less. The Exponential Distribution allows us to model this variability.
All that being said, cars passing by on a road won’t always follow a Poisson Process. If there’s a traffic signal just around the corner, for example, arrivals are going to be bunched up instead of steady. On an open highway, a slow tractor-trailer may hold up a long line of cars, again causing bunching. In these cases, the Poisson Distribution may still work okay for longer time periods, but the exponential will fail badly in modeling arrival times.
Note also that there is huge variability based on time of day: busier during commuting times; much slower at 3am. Make sure that your lambda is reflective of the specific time period you are considering.
Lambda then becomes a parameter of the model. And the higher the
- So everything random is not really random?
- Is anything random at all?
- Does seeing a pattern make it “not random”?
- Are we just Victims of Randomness and cannot do much else but put up with it?
Poisson Distribution as a 4As Complexity Idea…
Consider a coin toss. One gets HEAD(H) or TAIL(T), and if the coin is fair, the long term chances of getting a H or a T are even. If one tosses a single coin several times, one gets different sequences of Hs and Ts.
If we assume that an H means people get into their car and drive, what can we say of many many people? They are all tossing coins, so to speak, and leave only if they get a H. Each sequence of Hs and Ts is a manifestation of car traffic, with H being a vehicle, and T being no vehicle.
In a large society with
The Accumulated random binary Actions of a large number of people gives us an aggregate Poisson distribution for the occurrence of traffic, with a mean of
Is Randomness a Design Tool?

But we are interested in more than just the Poisson Process. And mangoes are far more interesting than cars!!!
- Do you remember plucking mangoes from the trees in your childhood gardens?
- Did you happen to be the youngest in the group?
- Did you have run home to get the salt + chilly powder?
- Why did you trust your friends not to eat off the best mangoes in your absence? ;-D
- Were you used to being the “denner” in every game?
- Or the last person to bat or bowl, or whatever was the cool thing in the game…
- Or did you do that “bat numbers” thing?
- Why did you trust your friends? ;-D
- What strategy did you use when playing “Rock, Paper, Scissors”? Were you always “steady as a rock”, or “variable as traffic”?
Perhaps you suffered, but maybe you didn’t because everyone “got their turn” and they weren’t always the first, nor were you always the last… So somehow it was all…fair, because it was “random”.
And you didn’t stick with just one of Rock, Paper, or Scissors. But chose one at…..random.
So can we use Randomness in Design? With intent? And is this the use of randomness in Art?
Pedagogical Vandalism
Let us throw some chalk pieces on the floor at random and see what happens!!
Was that a completely “mad” thing to do, throwing stuff on the floor? Or was it an act of Pedagogical Vandalism? (See wreck this Journal).
Is Randomness just too much to handle or comprehend?
Or can we “tame” it in some way, and put it to use in Art, Design, and Tech?
Have we been doing this all along? Have we been holding infinity in the palm of our hands, in the हाथ कीे लकीरे?
What diagrams or thought experiments can we create to do this?
WHY would this be a good idea? Is there a very Human Motivation behind this desire we might have?
Or let’s ask this lady here.

Wait, But Why?
- Randomness can help create fairness?
- Visibly?
- Generate Randomness to make things fair? How?
- What does that even mean, to “generate randomness”?
- If something is random-random, how can it be fair “every time”?
- What does “every time” even mean?
- Whom would you meet in a casino? In other words, what if something looks random, but isn’t really? See Reference 2 below.
We’ll see.
References
Seeing Probability Theory: https://seeing-theory.brown.edu/basic-probability/index.html A Superb visual website to see patterns in theory! Go and play there with Hamlet!
Penguin Press @ Medium. Abraham Wald and the Missing Bullet Holes. (Web Link)
R. J. MacKay and R. W. Oldford. Scientific Method, Statistical Method and the Speed of Light
Robert Scholz. May 1982. The Origin of Spread Spectrum Communications
Emma Neeson. 04 March 2023. Hedy Lamarr and the Frequency Hopping Spread Spectrum: The mother of Wi-Fi.
Karan Kashyap, Calculating the Value of Pi: A Monte Carlo Simulation, https://www.cantorsparadise.com/calculating-the-value-of-pi-using-random-numbers-a-monte-carlo-simulation-d4b80dc12bdf
Mozart Dice Game: Generate Mozart-like tunes by throwing dice: https://vician.net/mozart/
Theodore Sturgeon. (September 1957). The Pod in the Barrier. Galaxy Science Fiction. https://archive.org/details/galaxymagazine-1957-09/page/n9/mode/2up?view=theater